To, kar vemo, je kapljica, to, česar ne vemo, je morje.
Isaac Newton
V neskončnem matematičnem vesolju imajo formule osrednjo vlogo. Te matematične enačbe lahko najdemo v vseh matemtatičnih izrekih, od antičnih časov do nedavnih odkritij 20. stoletja.
Z vsako novo matematično enačbo, se nam poraja ogromno novih vprašanj, s tem pa prihajajo na površje tudi vedno novi odgovori.
V nadaljevanju so zbrani nekateri matematični izreki, enačbe in neenačbe ter formule, ki so spremenile naš pogled na svet.

Pitagorov izrek
Ta izrek sega nazaj v leto 530 pr. n. št. in je eden najbolj poznanih matematičnih izrekov, kar jih poznamo.
Enačba za pitagorov izrek je naslednja:
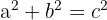
Pitagorov izrek je eden od temeljev sodobne matematike in je pomembno prispeval k razvoju matematike kot discipline. Tudi po dolgih letih ostaja formula tega izreka zasidrana v našem spominu.
v pravokotnem trikotniku kvadrat hipotenuze enak vsoti kvadratov drugih dveh stranic.
Pitagori in njegovemu izreku se lahko zahvalimo za enostavno računanje dolžine, kotov in tega, da vemo ali je trikotnik pravokoten ali ne. Ta izrek je le eden od mnogih primerov prikaza uporabe matematike v vsakdanjem življenju, če se tega zabedamo ali ne.
Pitagorov izrek se vedno znova uporablja v gradbeništvu, arhitekturi in mizarstvu, če naštejemo le nekatere.
Splošni gravitacijski zakon
navaja, da se dve telesi v vesolju privlačita s silo, ki je odvisna od njunih mas in razdalje med njima.
Gravitacijska sila med dvema telesoma je sorazmerna produktu mas obeh teles in obratno sorazmerna kvadratu razdalje med njunima središčema.
Na primer, Zemlja privlači Luno in obratno.
Enak zakon velja za privlačnost med jabolkom in Zemljo ali pa med planeti in Soncem: Splošni gravitacijski zakon.
Gravitacijski zakon in pa enačba, ki velja za eno najbolj prepoznavnih enačb v matematiki, je v 17. stoletju razvil Isaac Newton. Formula enačbe je naslednja:
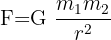
Where:
- F: Gravitacijska sila (N: Newtons)
- M: Masa prvega telesa (ponavadi planeta, kg)
- m: Masa drugega telesa (kg)
- R: Razlika med obema telesoma (meters)
- G: Gravitacijska konstanta
Gravitacijska interakcija je univerzalna in velja za vse vrste snovi. Izraža se le kot privlačna sila in ne povzroča odbijanja teles.
Teorija relativnosti
Matematika je, na nek način, poezija logičnih idej.
Albert Einstein
Formula za teorijo relativnosti je zagotovo ena najbolj znanih enačb, kar jih obstaja. Kljub temu je nihče ne razume v celoti.
Teorijo relativnosti je razvil Albert Einstein, ki je pomagal revolucionirati naše znanstveno razumevanje narave prostora in časa.
Ta teorija je ena najbolj znanih matematičnih teorij, enačba pa gre takole:
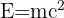
Ampak, na kaj se ta enačba nanaša?
Najprej je pomembno omeniti, da je masa katerega koli objekta oblika energije. V formuli se lahko masa (𝑚) objekta pretvori v energijo (𝐸) in obratno. Črka "c" predstavlja hitrost svetlobe, ki je kvadrirana, da ponazori, kako lahko že majhna količina mase povzroči veliko količino energije.
Ta formula, ki ponazarja teorijo relativnosti (posebno in splošno relativnost), je revolucionirala naše dotedanje razumevanje fizike.
Še danes ostaja ključna, saj dokazuje, da se snov lahko pretvori v energijo in obratno 🤓.
Posebna teorija relativnosti je uvedla idejo, da je hitrost svetlobe univerzalna konstanta, ki se ne spreminja, ter da čas ne teče enako za telesa, ki se gibljejo z različnimi hitrostmi.
Teorija relativnosti je najbolj znana matematična teorija na svetu zato, ker je dokazala kako pomembna je matematika v vsakdanjem življenju in kakšen vpliv lahko ima matematika skozi čas.
Ploščina kroga

Krog je zaprta ravna krivulja, pri kateri so vse točke enako oddaljene od središča. Preprosto povedano, krog je zaprta črta, podobna obroču ali pnevmatiki.
Enačba je naslednja:
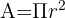
Kjer je
𝐴 = ploščina kroga.
Nato imamo število π (π = 3.1416)
in 𝑟, ki predstavlja polmer kroga. Polmer kroga je razdalja med središčem kroga in katerokoli točko na krivulji.
Ploščina kroga je zelo pomembna, bodisi za praktične namene, kot je slikanje okrogle mize, ali v fiziki
Ploščina kroga nam je omogočila preučevanje valovnih dolžin, elektromagnetičnega polja in leče ter celo porazdelitev svetlobe.

Teorija kaosa
Teorija kaosa je znanost o nepričakovanem, nelinearnem in nepredvidljivem. Je ena najbolj znanih matematičnih teorij.
Ta teorija obravnava nelinearne pojave, ki jih je praktično nemogoče napovedati ali nadzorovati, kot so turbulenca, vreme, borzni trgi, možganska stanja in še več. Ti pojavi so pogosto opisani s fraktalno matematiko, ki odraža neskončno kompleksnost narave.
Teorija kaosa zajema na primer učinek metulja. Ta učinek je pogosto opisan takole: zamah metuljevih kril v Avstraliji lahko povzroči orkan v Čilu. Sliši se kot fantazija, kajne? Vendar teorija kaosa omogoča obstoj tega pojava. Natančneje, učinek metulja pomeni, da lahko majhne spremembe začetnih pogojev privedejo do drastičnih sprememb v končnem izidu.
Naša življenja so neprestana demonstracija tega načela. Ker nikoli ne moremo poznati vseh začetnih pogojev kompleksnega sistema v zadostni meri, ne moremo pričakovati, da bomo natančno napovedali njegov izid. To je lahko v neposrednem nasprotju z idejo uporabe matematike pri pokru ali igrah na srečo, saj že majhne napake pri merjenju stanja sistema lahko povzročijo ogromna odstopanja in s tem naredijo vsako napoved neuporabno. To je ena izmed najbolj fascinantnih matematičnih teorij.
Eulerjeva enačba
Eulerjeva enačba se glasi:
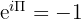
Mnogi matematiki in strokovnjaki to enačbo smatrajo za eno najosupljivejših, kar jih je bilo kdaj ustvarjenih.
Ni izjemna le zaradi svoje elegance, temveč tudi zato, ker v eni sami formuli povezuje pet ključnih matematičnih konstant:
- e: osnova naravnih logaritmov
- i: imaginarna enota
- π: 3.1416
- 1 in 0: cela števila
Eleganca Eulerjeve enačbe leži v njeni preprostosti.
💡Prav zaradi te preprostosti je imela velik vpliv na področja, kot so inženirstvo, teorija števil in kompleksne funkcije.
V eulerjevi enačbi je e Eulerjevo število, osnova naravnih logaritmov, i imaginarna enota, ki zadošča pogoju i2 = −1 in π, število pi, ki predstavlja razmerje med obsegom kroga in njegovim premerom.
Drugi zakon termodinamike
Prvi zakon termodinamike določa, da se energija lahko prenaša med fizičnimi sistemi v obliki toplote in dela. Drugi zakon pa uvaja drugo količino, znano kot entropija.
Gre za princip sprememb in evolucije, saj določa, v katero smer so možne pretvorbe potencialne energije.
Zato so nekatere kemijske transformacije možne, druge pa ne. Z gotovostjo lahko na primer trdimo, da če v skodelico vroče kave potopimo kocko ledu, se bo ta stopila, medtem ko kava nikoli ne bo zmrznila.
Drugi zakon termodinamike je fizikalno načelo, ki omejuje smer procesov prenosa toplote med telesi. Razvit je bil na podlagi posploševanja eksperimentalnih dejstev in je bil večkrat eksperimentalno potrjen.
Bolj preprosto povedano, ta zakon pravi, da ni mogoče, da bi bil edini rezultat nekega procesa prenos toplote iz hladnejšega telesa na toplejšega.
Čeprav je k oblikovanju načel tega zakona prispevalo več znanstvenikov, sta za glavno prepoznavnost poskrbela Ludwig Boltzmann in Max Planck, leta 1873. Ta zakon uvaja koncept entropije, ki določa smer pretvorb energije.
Pomislimo na ledeno kocko, ki jo potopimo v skodelico vročega čaja.
Kaj mislite, da se bo zgodilo?
Točno tako, led se bo stopil.
Drugi zakon termodinamike pojasnjuje, zakaj se bo to zgodilo in ne obratno - led ne bo zamrznil skodelice čaja.
Schrödingerjeva enačba
Ta enačba je ena najbolj znanih formul v matematiki. Ne, tokrat ne govorimo o mački, ampak o eni izmed drugih Schrödingerjevih briljantnih idej (prejemnik Nobelove nagrade za fiziko).
Schrödingerjeva enačba je ključna za razumevanje, kako se delci spreminjajo skozi čas. Pomaga nam opisati različna stanja, v katerih se delec lahko nahaja.
Poleg tehničnega pomena ta enačba odpira tudi fascinantno filozofsko vprašanje: Ali je snov res sestavljena iz konkretnih fizičnih stanj, kot so trdno, tekoče in plinasto, ali pa gre za nekaj več? Z drugimi besedami, vabi nas k razmisleku o sami naravi snovi in o tem, kako jo zaznavamo. Takšne matematične uganke so zelo pogoste, ta enačba pa predstavlja vrata do odgovorov, ki jih bomo nekoč odkrili.
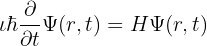
Schrödingerjeva enačba je bila izjemno uporabna za razvoj jedrske energije, računalništva in laserskih tehnologij.
Zahvaljujoč tej enačbi, eni najbolj znanih matematičnih enačb v zgodovini, smo lahko bolje pojasnili obnašanje atomov in subatomskih delcev.
Schrödingerjeva enačba opisuje spremembe delca skozi čas. Določa stanja delca, iz katerih je mogoče opisati katerokoli stanje.
Ta enačba odpira pravo filozofsko vprašanje: ali je snov sestavljena iz možnih fizičnih stanj (trdno, tekoče, plinasto)?
Maxwellove enačbe
Štiri Maxwellove enačbe sestavljajo eno najpomembnejših osnov sodobne fizike. Te enačbe so imele velik pomen tako za elektrodinamiko kot za teorijo relativnosti.
Maxwellove enačbe so naslednje:

Odkritje Maxwellovih enačb velja za vrhunec klasične fizike, saj je mogoče iz njih izpeljati vse enačbe elektromagnetizma. Te enačbe opisujejo interakcijo med električnimi in magnetnimi polji ter njihov odnos do električnih polj in nabojev. Tako električna kot magnetna polja je mogoče grafično prikazati s pomočjo diagramov silnic. Njihov vpliv na sodobni svet matematike je neizpodbiten, saj dokazujejo, da je matematika nepogrešljiv del naše družbe.
Grafično gledano obe polji predstavljata delovanje sile na naboje. Preprosto povedano, električna in magnetna polja so medsebojno povezana. Vplivata drug na drugega in se lahko spreminjata.
Te znamenite enačbe so močno prispevale k razvoju matematike. Niso le znanje same po sebi, temveč so omogočile tudi nastanek in izpopolnitev drugih matematičnih konceptov.
Vse te slavne matematične enačbe imajo nekaj skupnega: so preproste (v smislu elegance), jedrnate in povezujejo temeljno matematiko z enostavnejšimi koncepti. Vsaka od teh enačb ima obsežne in globoke uporabe v vsakdanjem življenju in različnih disciplinah, kar jih naredi izjemno dragocene. Čeprav je matematika lahko zapletena, ostaja hkrati tudi izjemno fascinantna.
Jezik matematike je univerzalen. Ne glede na to, ali govorite angleško, francosko ali špansko – če razumete jezik matematike, se boste lahko sporazumevali v katerem koli jeziku. Ta jezik je zasnovan tako, da nam omogoča odkrivanje vesolja z enim samim izraznim sredstvom: jezikom matematike.
matematičnih raziskav!
Povzetek z umetno inteligenco:















